telegraphic codes and message practice |
|||
margins : |
chess codes |
||
chess codes |
Chess codes are a kind of topographic code. Two are described below. The chess pieces, their respective functions and the associated rules of the game together provide a kind of dictionary and syntax for describing shapes and outlines on an 8 x 8 = 64 unit board. The board itself becomes the all-important memory device — cache memory, so to speak — to which all instructions must refer. For cognate means of describing areas and curves telegraphically, see elementary signs : letters, specifically:
|
Gringmuth's Telegraphic Code
|
|
|
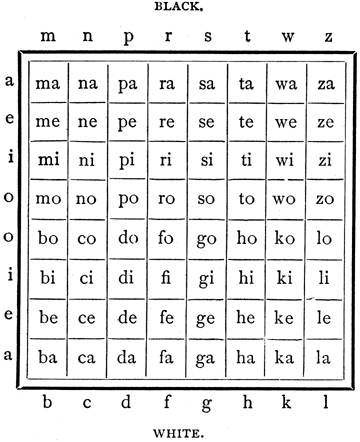
This code is the invention of Mr. D. Gringmuth, a leading Russian problem composer, and has been adopted in several matches. An account of it may be found in La Strategie, the Times-Democrat of New Orleans, The International Chess Magazine, and the Chess Players' Annual. By means of it two different moves can be combined in one word for transmission. If telegraphing only one game the first two syllables would represent White's move, and the last two syllables Black's answer. In the match between London and St. Petersburg, in which two games were simultaneously contested, the first two syllables represented the move in the game in which the party sending the dispatch had the first move, and the two last syllables the move of the same party in the game in which their adversaries had the first move. The squares are designated in the following diagram [see above], and each move is designated by giving the square from which the piece or pawn is moved, followed by the square to which it is moved. By an extension of the code suggested by E. D. Nores in the Times-Democrat, the letter c, added to the last syllable, designates "check;" similarly p means "take pawn en passant;" l added to the symbols for the King's and Rook's squares, means Castles; q, r, b, k, added to the last syllable indicate that a pawn reaching the last row becomes respectively a queen, rook, bishop, or knight ; and finally m means mate, and s, stalemate. Thus Game No. 2, in Philidor's Defence, p. 154, would be recorded as follows for telegraphing: — Gegoseso Kahireri Fefoteto Fosottogo Hiworiro Sosiwazi Cadipepi Wogorogo Fazowewi Zosozawa Daworari Bafarisi Hadonare Dosi. ex William Steinitz. The Modern Chess Instructor, Part 1. New York and London, G. P Putnam's Sons, 1889 : xix See also Knight's Tour Notes compiled by George Jelliss (Knight's Tour Recreations involving Words or Letter) In most cases, the codewords are eight-letter ciphers reminiscent of those in the Bauers Code (1913), e.g., abababal. In addition to their dada-like sound, they also resemble Japanese words such as might be enunciated — with the fullest exploration of every syllabic nuance — in Noh drama.
|
Edwyn Anthony, Chess Telegraphic Codes (1890)
|
|

|
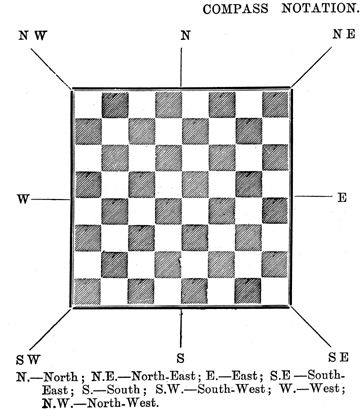
"This notation, valueless for ordinary use, is excellently adapted for telegraphic purposes. We do not know with whom it originated, and we have ventured to apply to it the epithet 'compass' as indicative of its nature. "Excluding the Knight, whatever piece or pawn be moved it must move in one of the eight directions marked in the diagram at the side ; and these directions may be conveniently denoted in the way in which they are indicated on the mariner's compass. Thus King N1 = King one square upwards ; Queen's Bishop S W 5 = Queen's Bishop five squares diagonally downward to the left, etc. And, since plainly no piece can move more than seven squares at one time, the indicating number will never exceed 7. Similarly, the Knight, wherever he stand, can only move in eight different directions, as illustrated by the next diagram…" |
"Thus 'King's Knight 5' indicates a move of the Knight in the direction shown by the diagram ; and as the Knight's move is always the same except in direction, it constitutes a sufficient description of the moves of that piece. Thus we see that, if we know the square on which a piece or pawn stands, the 'Compass Notation' forms an adequate indication of every possible move. For example, if the Queen be on K's 5th square then 'Queen N E 3' denotes "Queen to K R 8.' Again, if the King's Rook stands on his own square, 'King's Rook, W 7" = 'K R to Q R sq.' etc. When a game is played over from start to finish, it is evident that the position of the pieces at every stage is known ; and, therefore, that the notation just described may be used for recording games." |
Anthony provides a Figure and related Word code. Both of these incorporate the Compass Code described above. He presents only two sample pages of the word code, as a prospectus to an envisioned publication at larger size (in which those two pages would fit onto one). The word code is based on an elemental dictionary of 315 instructions; of these, 268 are sufficient to describe the movement of any piece on the board, so long as its current position is known, thanks to compass notation. Five instructions relate to endgame situations (resigns, drawn, lost by exceeding time limit, adjourned, and "blank"). Forty-one terms are reserved for names of players, or other information. Each code word denotes two moves. It does this as follows : "Turn the word up as in a dictionary. Then Move A is the move at the top of the page containing the word ; and Move B is the move given in the line in which the word occurs." For the reverse — find the single word denoting two moves — one turns to the page with Move A listed at top, and then finds on that page Move B. The required code word will be found next to the latter. The figure code condenses into one all of the move-pairs that fill up 315 pages of the word code. It incorporates the same 315 instructions provided on one page of the word code. The first move has a six-figure name in Table Column 1. The second move or instruction is described by one of 315 figures, 1-135. One adds that number, e.g., 77, to the first figure to find the cipher for the two moves. Anthony's explanation of the translation is clear enough: In Table A, find the two numbers between which th egiven number lies. The move contained int he same line wit hthose numbers will be the move orresponding to Table A. Subtract the smaller of the said two numbers from the given number. The remainder will always be found somewhere or other in Table B; and the move in the same line with it will be the move corresponding to Table B. Example. Given the number 43663. ¶ The given number lies between 43609 and 43925. The Table A move is, therefore, "King's Bishop S W 3." ¶Subtract 43609 from 43663, and the remainder is 54. ¶ The Table B move is, therefore, "Queen W 2." |